I just caught this genius talk from Dan Meyer on teaching maths, and more generally, problem-solving. It appealed to me because of the emphasis on learning through concrete things, not abstractions.
Watch for the way students are hand-fed the answers in conventional learning environments. In one case, an otherwise-fine worded problem concludes with a parenthesised reference to a similar problem. In another problem, the ski lift, the modelling is provided at the same time as the question is asked.
Meyer’s main point is that worded problems should feel real, and students should really sit there and struggle with them for a while. He uses the example of a water pump - how long does it take to fill up? Great question, but the typical math textbook presents it in this weird abstract and wordly way:
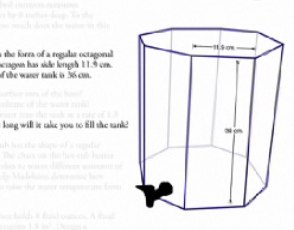
This is the 21st century, so we can better represent the problem like this:

The whole problem is just a photo and a simple question. Now you have something you can struggle with. Eventually you’ll get sick of talking in long-winded ways about the concepts and you’ll start to introduce abstract modelling. The modelling comes from the conversation, not vice-versa.
But wait, we said this is the twenty-first century, so Meyer goes one better and actually shows a video of the water tank filling up.

Now it’s filling up agonisingly slowly, and all the students have successfully been baited into really wanting to know when will this thing end. They are on equal footing when coming up with intuitive guesses and the mathematical modelling falls from that.
This all reminds me of the tension you’re supposed to feel when reading the problem and forces of a design pattern. You’re supposed to feel a little queasy as you realise how all the forces are in conflict with each other, and then the sense of relief from the answer that resolves the tension.
I’ll finish off with Meyer’s practical tips:
- Use multimedia
- Encourage student intuition
- Ask the shortest question you can
- Let students build the problem
- Be less helpful </ul>

